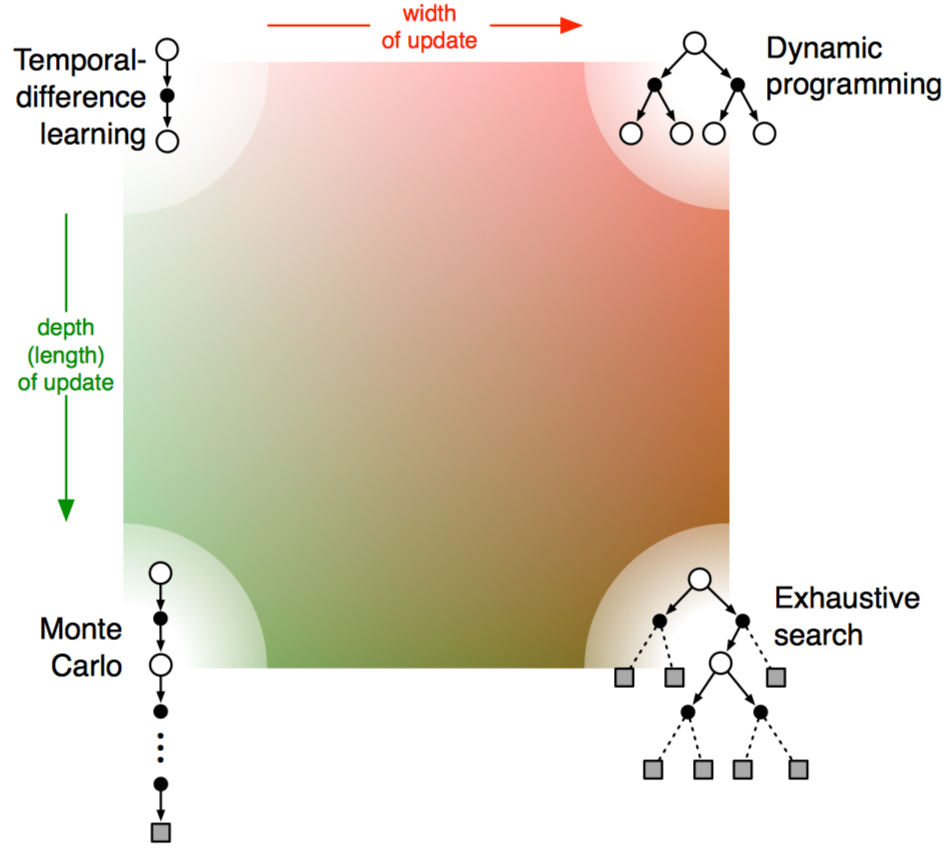
Chapter 8 Planning and Learning with Tabular Methods
之前的章节中学习了基于模型的方法(model-based)和模型无关的方法(model-free)。基于模型的方法使用planning方式,而模型无关的方法使用learning的方式。这一章中试图将这两种方法整合起来。
8.1 Models and Planning
model:
- distribution model(分布式模型)
- sample model(采样模型)
experience:
- real experience(真实经验):从真实模型产生
- simulated experience(模拟经验):从学习到的模型产生
planning:
- state-space planning(状态空间搜索)
- plan-space planning(规划空间搜索)
其中,状态空间搜索使用如下方式,前面的动态规划方式就是一种状态空间搜索:
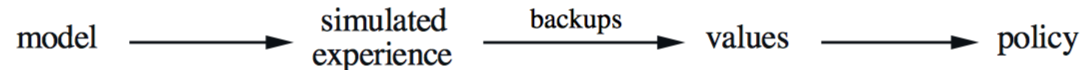
其实,planning与learning的区别仅在于,planning使用模型经验,learning使用真实经验。一个用于planning的q-learning算法,random-sample one-step tabular Q-planning,如下所示:

8.2 Dyna: Integrated Planning, Acting, and Learning
从真实经验直接学习策略称作direct RL,从真实经验学习模型,再通过模型规划策略,称作indirect RL。间接学习的方式充分利用了实际经验,得到的策略更精确;而直接学习的方式更加简单,不受学习模型误差影响。结合直接学习和间接学习的方法称作Dyna-Q方法。
在Dyna-Q中,planning方法使用random-sample one-step tabular q-planning,直接学习采用one-step tabular q-learning,模型学习使用基于表格的方法,并且假设环境是固定的。一般来说,这几个过程是可以并行进行的。一种通过的架构如下:
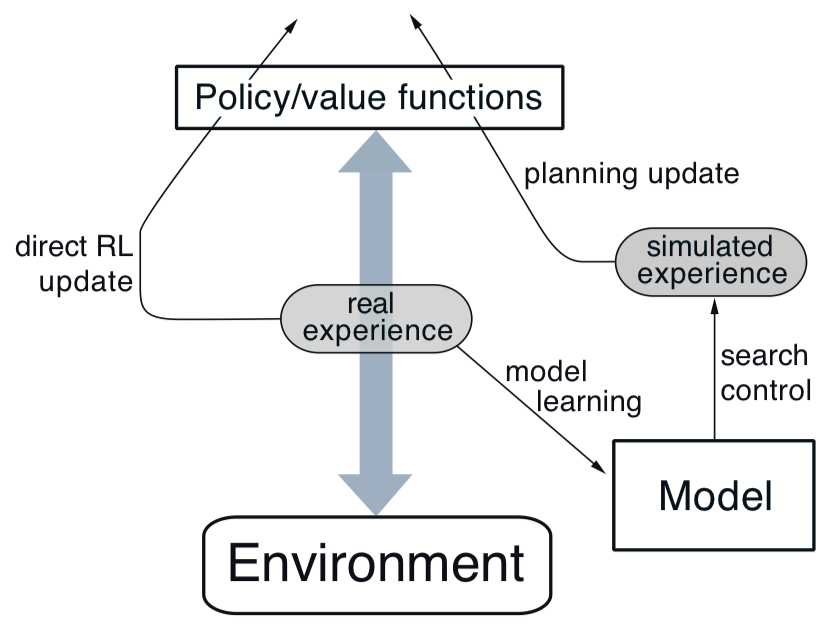

8.3 When the Model Is Wrong
当环境是动态变化的,模型学习过程可能并不精确。因为只观测到了少量采样样本,并且已经过期,这样只会学习到次优策略。因此需要考虑的仍然是平衡exploration和exploitation,使得agent可以适应环境的变化。一般而言,这种平衡过程无法达到两个最优,但是简单的启发式过程已经可以十分有效。
改进后的Dyna-Q方法称作Dyna-Q+。经历的时间的越长,样本越容易发生改变,模型越容易出错。因此,在模拟经验中引入“bonus reward”,每一个动作转移产生的奖励为$r + \kappa \sqrt { \tau }$,其中,$\tau$为这个转移被忽略的时间长度。这种方式可以通过鼓励探索的方式修正学习模型的偏差。
8.4 Prioritized Sweeping
在Dyna算法中,planning使用随机uniform采样的方式,效率较低;使用优先级扫描(prioritized sweeping)可以只关注一部分特殊的状态-动作对。
这里使用一种方向传播算法,称作“backward focusing”,即首先更新那些需要紧急更新的状态值函数,并且进行回退,即如果子节点发生变化,父节点也会发生变化。这里的紧急度(urgency)使用TD error来衡量。
优先扫描算法:维护每个状态 - 动作对的优先级队列,按照估计值变化的大小排列,每次取出变化最大的状态-动作对进行更新,进一步将其每个前任加入队列,并计算估计值变化。

优先扫描的一种扩展形式:模型学习过程中保存所有状态-动作对及其被访问过的次数;在更新值函数过程中,使用expected update,而不是sample update。
优先扫描虽然提高了planning的效率,但仍然具有局限性,即在随机环境的情况下,使用期望更新的方式可能会浪费很多计算资源在小概率转移上。实际上,还有跟多策略可以选择,如“forward focusing”等。
8.5 Expected vs. Sample Updates
目前所学到的很多值函数更新方式都可以按照以下三个维度分类:1. 状态值函数or动作值函数;2. 最优策略or给定策略; 3. 期望更新or采样更新。如下图所示:
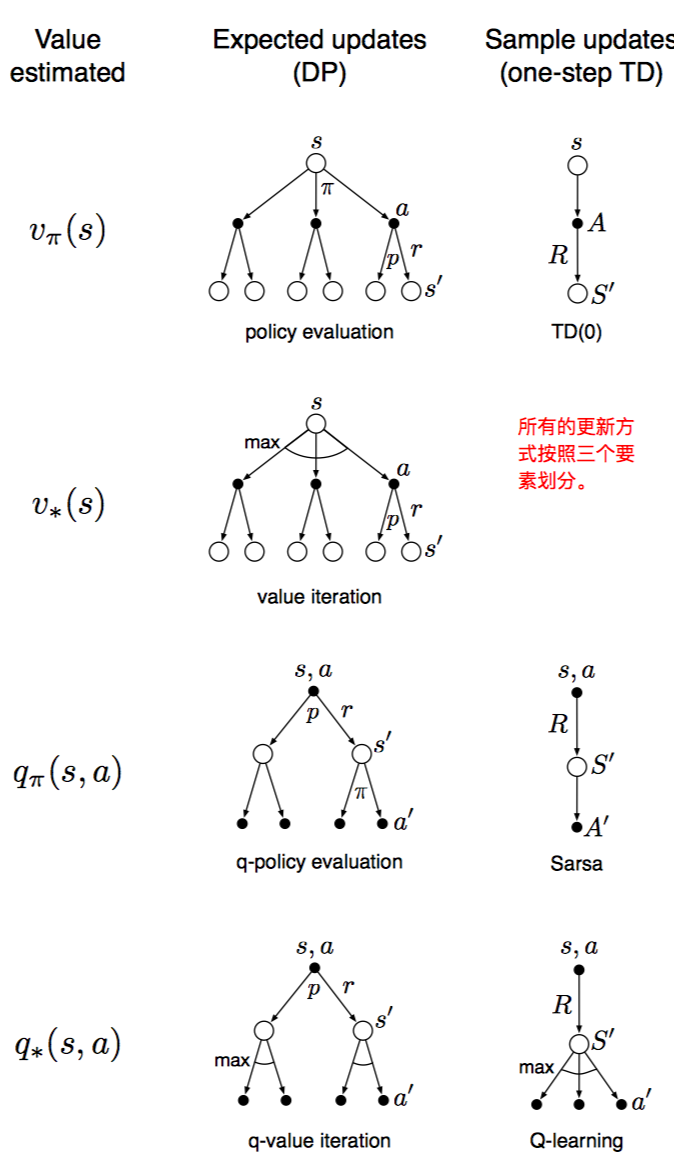
期望更新和采样更新的主要区别在于环境是随机的情况下。期望更新计算更加精确;而采样更新会受到误差影响。另一方面,采样更新计算更加简单。一般而言,有足够时间的情况下,推荐期望更新;时间不充裕的情况下,推荐采样更新。即采样更新适用于下一个状态随机变化较大,或者有很多状态需要解决的情况。
8.6 Trajectory Sampling
这一节主要比较两种分布式更新方式,一种是传统的动态规划,即每次扫描中更新所有状态值函数。另一种是基于某种分布从状态空间中选取状态值函数进行更新。
这种分布可以使Dyna-Q中的uniform分布,不过这就和动态规划中的完全扫描没有什么区别了。一般是基于某个策略而观测到的采样分布,简单可行。这种方式也称作轨迹采样(trajectory sampling)。
基于在线策略采样得到的分布,在初期更新更快得到更好的效果;但长期的时候,因为受到误差的影响,较uniform的效果会有所减弱。一般而言,推荐使用在线策略的分布,更适合大型问题。
8.7 Real-time Dynamic Programming
实时动态规划(RTDP)是一种基于在线策略轨迹采样的动态规划值迭代算法。其也是一种异步DP算法。
最终得到的是最优部分策略(optimal partial policy),即对于相关状态的最优策略,但无关状态的动作选择是未定义的或者随机的。并且,RTDP保证收敛到最优部分策略,不需要对每个状态访问无限次,甚至某些状态从来没有访问过。这种方式适用于状态数量较大的情况。
还有一些扩展情况,如用于stochastic optimal path problems的“learning real-time A*”算法。
RTDP另一个优点:其值函数达到最优值函数,并且其用于生成轨迹采样的策略也是最优策略。因为这个策略对于当前值函数而言总是最优的,并且最优策略可能在值函数并不是最优的时候提前形成。在传统DP中检查策略是否最优是一个额外的工作。
随着学习的继续,RTDP的关注范围越来越窄,最终只会关注那些最优策略上的状态。
8.8 Planning at Decision Time
planning包括两种方式,一种是之前的动态规划,Dyna等算法中提到的,利用模型从模拟经验中获得最优策略。即不断从表格中更新值函数,或者从很多状态中,选择最优动作,称作backward planning。
另一种为decision-time planning,即遇到每一个新状态,再去进行planning过程,即比较所有动作后下一个状态值函数的大小。
backward planning无法关注到当前状态,而decision-time planning关注于当前的具体状态。一般情况下,decision-time planning在每次选择具体动作后,都会将创建的值函数丢弃,这并不会带来十分大的损失,因为状态空间可能十分大。决策时规划通常用于不需要快速响应的系统。
8.9 Heuristic Search
启发式搜索是基于decision-time planning的一种状态空间规划算法。
对于当前状态S,从叶子节点的值函数反向传播到当前状态节点停止。经典的启发式搜索算法,并不改变值函数,而只寻找策略,因此,所有的值函数回退值被丢弃。
使用启发式搜索方式可以获得更好的策略。假设目前有准确的模型和不准确的价值函数,则使用更深的扫描,可以得到更好的策略。扫描深度为任务长度时, 策略最优。但扫描越深,消耗时间越长。因此,具体任务应该选择合适的深度。
启发式搜索只关注与当前状态相关的状态和动作,因此只需要更少的内存和计算资源。
除了策略选择,对于值函数更新可以选择类似的方式,即通过深度优先的启发式搜索方式,自底向上进行更新。这种更新方式并不在于将大量单个异步更新拼凑在一起,而是使得当前状态和子状态的更新更加集中。
8.10 Rollout Algorithms
rollout算法是基于MC控制的decision-time planning算法。该算法基于某个策略rollout policy,使用MC估计当前状态的动作值函数。注意在MC控制中估计完整的动作值函数。
具体实施中,对于当前状态的每个动作,计算返回值的均值,得到动作值函数的估计。取最大动作值函数所对应的动作作为当前状态的策略。这种方式一定会得到更优的策略。其也可以看做动作规划中的一步策略迭代算法。也就是说,rollout算法目的在于提升rollout策略,而不是找到最优策略。
但这种方式仍然会陷入平衡关系,好的rollout策略需要更多的模拟过程;但在decision-time planning中,时间限制往往十分严格。对此,有以下解决方案:1. 并行模拟多个试验;2. 将一个片段切分成很多短片段,对每个短片段返回值进行学习;3. 修剪掉那些不太可能是最优策略的候选动作。
该算法虽然不是学习算法,但应用到了强化学习的很多特性,如MC控制。
8.11 Monte Carlo Tree Search
蒙特卡洛树搜索是当前应用decision-time planning比较成功的一个案例。同样,在遇到每一个新状态时,MCTS被激活用于选择动作。
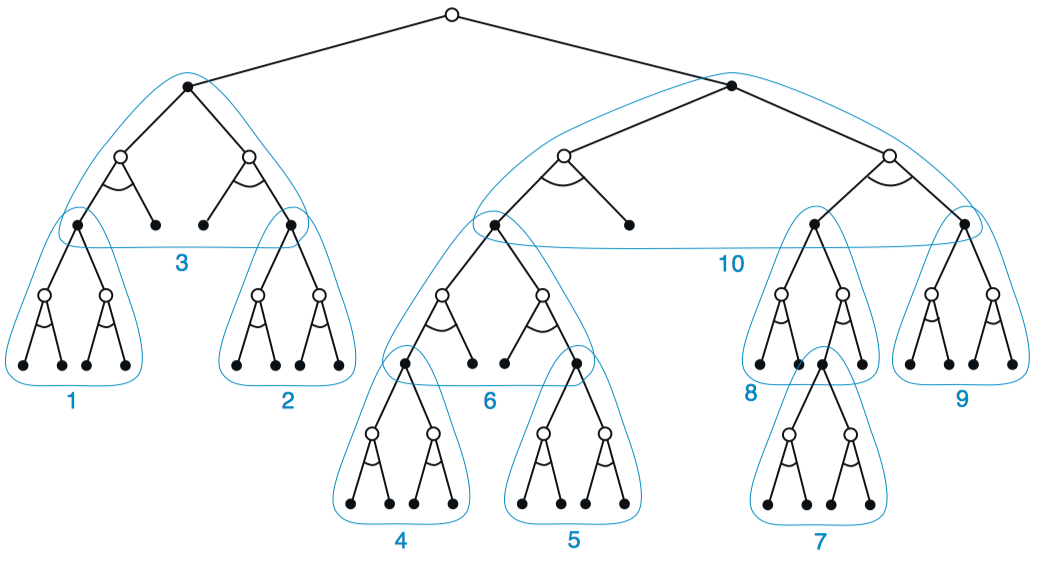
大多数情况下,用于生成模拟片段的策略称作rollout policy。任何模拟片段都会自顶向下穿过树,并从某个叶子节点退出。在树种的状态,使用tree policy选择动作,这部分时可以被优化的;而退出叶子节点后的动作选择使用默认的rollout policy。
其中,tree policy常常需要平衡探索和开采过程,一般使用$\epsilon-greedy$策略或者UCB规则。
具体而言,MCTS的每一个迭代包含以下步骤:
- 选择:使用tree policy,选择从根节点到叶子节点的所有动作
- 扩展:一些情况下,从叶子节点继续向下扩展一两个子节点,代表尚未被探索过的动作。
- 模拟:从选择的叶子节点,或者被扩展的新节点开始,使用rollout policy完成一个完整的片段模拟。
- 回退:计算模拟片段的返回值,并追层回退更新直到根节点。注意rollout policy选择的动作对应值函数并不被保存。
在重复迭代若干次后,从根节点开始,基于树种保存的数据使用某种策略选择每个动作,可能是最大值函数对应的动作,也可以是最大访问次数对应的动作。
MCTS实际是一种rollout算法,其基于在线学习,增量学习,采样学习的方式实现策略提升,此外,MCTS还将树内的动作值函数保存下来,并采样更新。
8.12 Summary of the Chapter
这一章结合了planning和learning的方法,提出了多种综合的强化学习方法。
此外,对于多种的state-space planning methods,可以划分为几个角度。一个维度是更新的大小变化,如sample update和expected update;另一个维度是更新的分布变化,如Prioritized sweeping关心值函数变化的状态,On-policy trajectory sampling关注更可能在实际环境中遇到的状态。
此外,planning还可以使用在更多的情况,如decision-time planning方式。
8.13 Summary of Part I: Dimensions
这一部分主要介绍了基于表格的多种强化学习方法,它们都有一些共同点:1. 估计值函数;2. 基于状态轨迹完成值函数回退更新;3. 遵循GPI策略。
此外,这些方法在以下几个维度上互相区分:1. 使用sample updates或者expected updates;2. 更新的深度,即自引导的度;3. on-policy还是off-policy策略。